House Prices - Advanced Regression Techniques
This project was a submission to a Kaggle competion with the goal of predicting the sale price of houses. At the time of writing, the code scored in the top 5% of the leaderboard. You can read more about the Kaggle competion and access my public notebook at:
I'm going to refrain from filling this page with Python code as it can be accessed in the notebook above. Instead, I will walk through the process of creating the predicitive models that were used and focus on some of the insights and decisions that were made.
Exploratory Data Analysis (EDA)
Perhaps the most important part of any machine learning project is understanding the data you're working with. As you will see later, implementing and training models is relatively easy and generally takes just a few lines of code. Most of the work is in collecting and appropriately modifiying the data that will feed those models. In this case we are provided with the data we will use for the competition, but will need to understand how it will need to be changed to be most useful to our models.
The provided training data has 1460 rows and 81 columns. One column is the predicition target (sale price) and one is an ID column, so in total we have 79 possible features to use.
Data Distribution
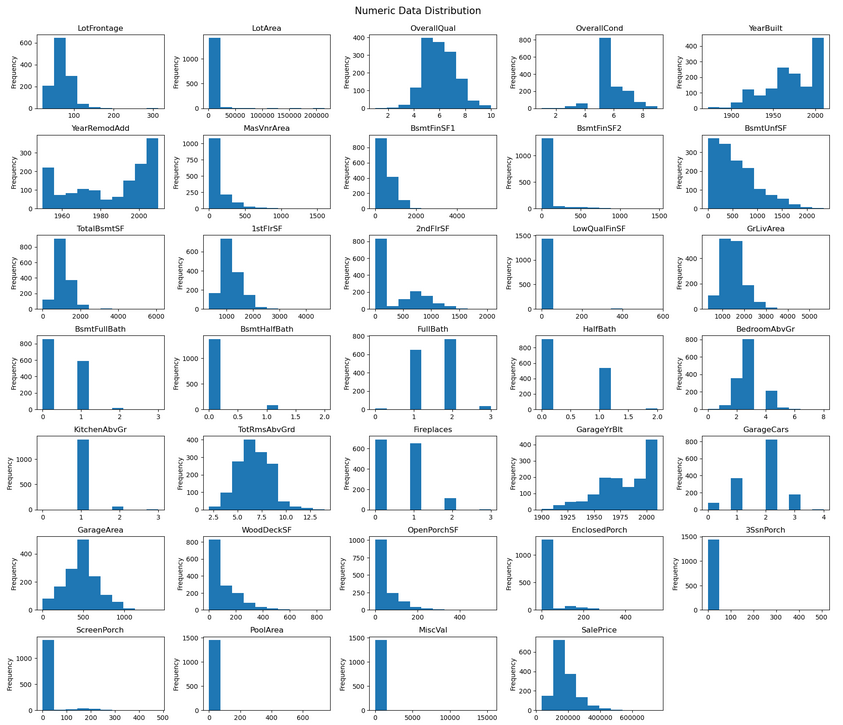
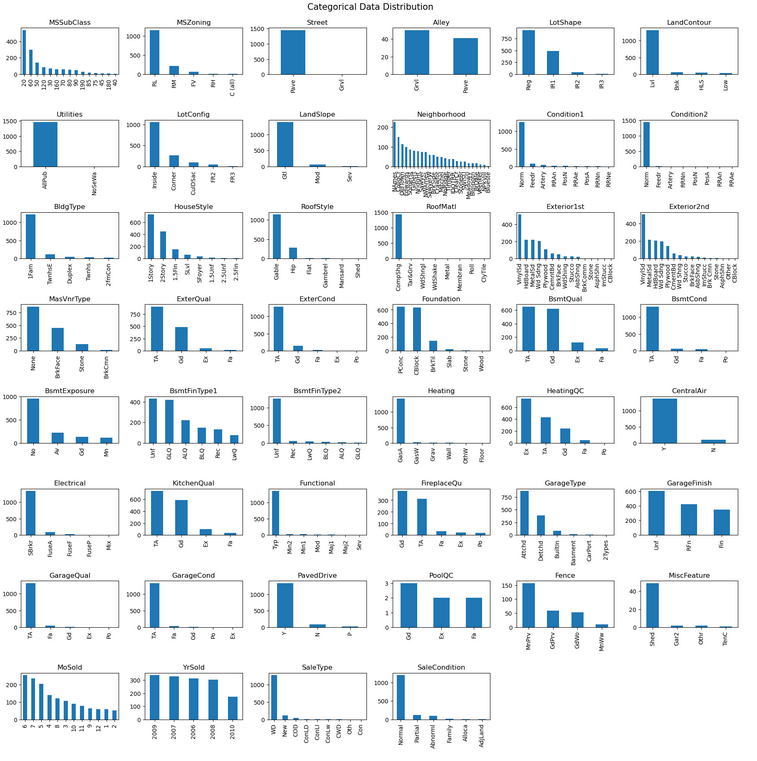
Below are the univariate distributions of all our features. We would ideally like to see a normal distribtion for the numeric features, but it looks like there is a high degree of skew in some of the charts. For example, "BsmtUnfSF" has a large positive skew, along with several others. This is something we will try to fix.
In the categorical data, we can see many features with very uneven distributions among the various categories. If we look at "Street" in the top row, nearly every row has a value of "Pave"; "Grvl" is almost never present in the data set. "Condition2" has a similar distribution. It may be difficult for a model to gain any predictive value from a catageory that only has a row or two of data.
Outliers and Correlation
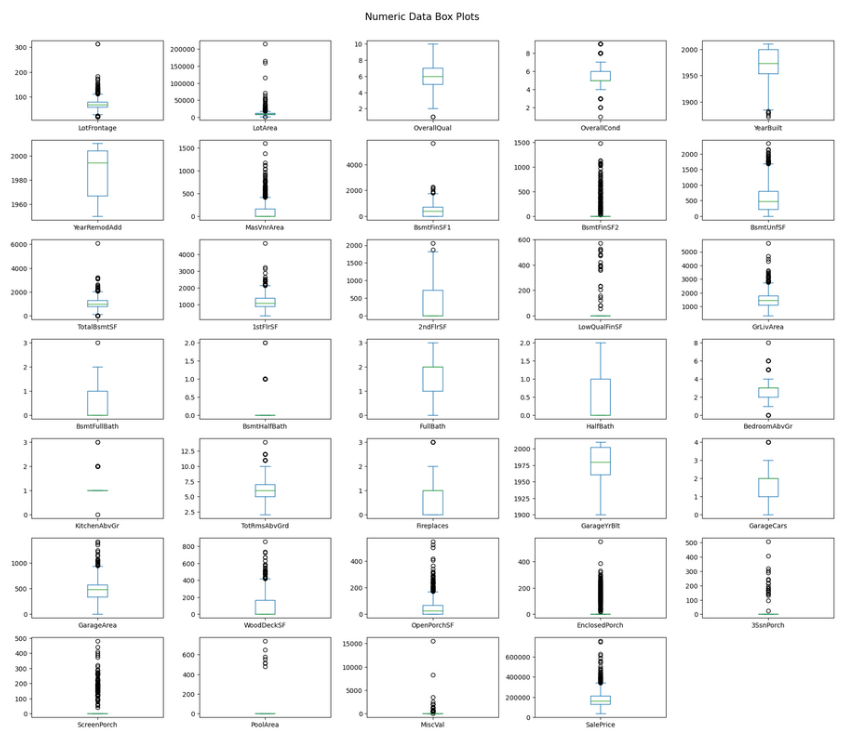
Another way to look for possible outliers in the data is to use a box plot. Box plots show a few key values related to each feature. They are:
- The minimum value (excluding outliers)
- The maximum value (excluding outliers)
- The median
- The first quartile
- The thrid quartile
Outliers are determined based on the interquartile range. The circles on the chart to the left could be considered outlier. There are a lot! A lot of these are due to the highly skewed distribtions. In columns that have almost entirely one value, anything that is not that value could be considered an outlier.
If we had a lot of data to work with we could try dropping some of these points. However, since we only have ~1400 rows to start with, we will leave most of the points in for now.
Relationship to Sale Price
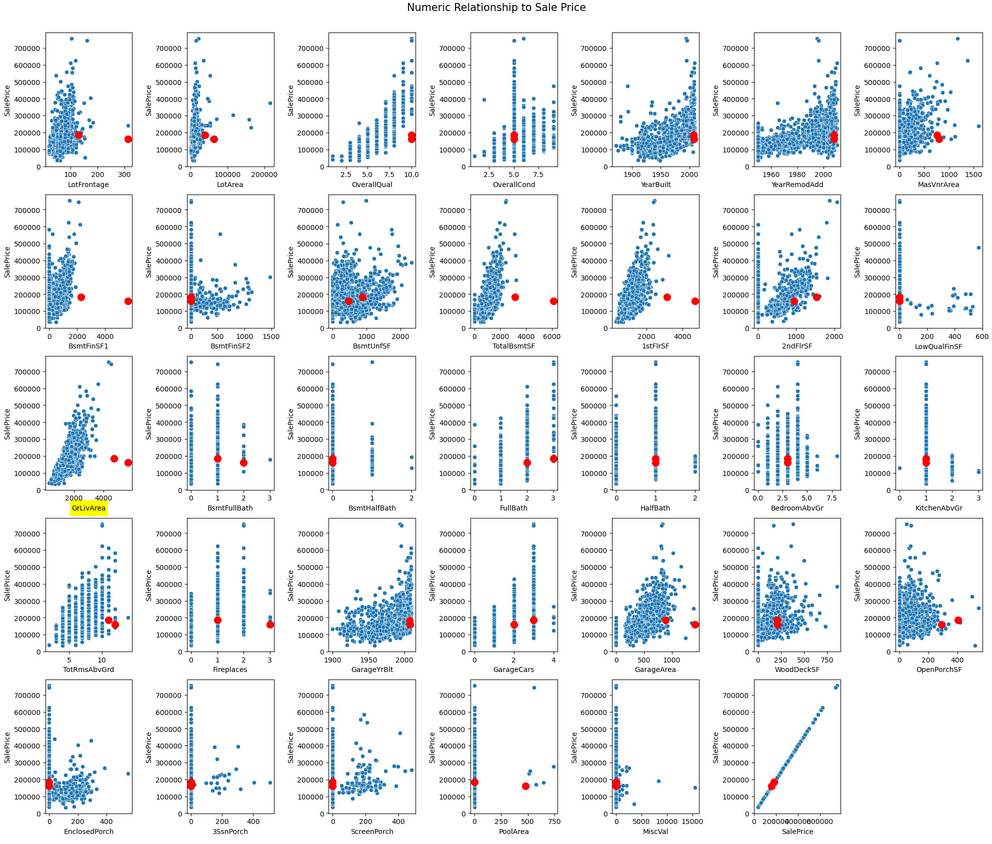
This chart shows the relationship between our numeric features and the target. Highlighted in red are two points that will be removed.
Take a look at the highlighted "GrLivArea" chart. We have a seemingly pretty linear relationship between the size of the home and the sale price, except for these two points which go against the trend. They also negatively impact another highly correlated feature, OverallQual, where these two points represent very high quality homes with a low sale price. Removing them will create a stonger relationship between these features and the sale price, which will hopefully give us better predictive ability for the large majority of houses.
Relationship to Other Features
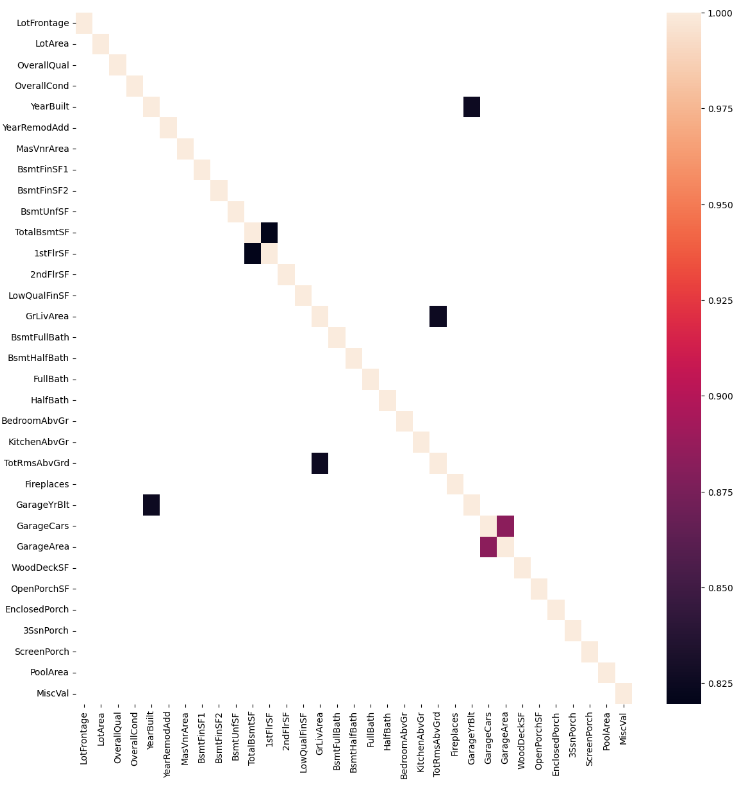
Here we can see the linear correlation between each feature and all other numeric features. Correlation values >0.75 are shown as colored blocks on the chart. The chart indicates that there are several features which are highly related to one another. For example, "GarageCars" and "GarageArea". GarageCars tells us how many cars the garage holds. It makes sense that as the garage area gets bigger, the number of cars it can hold increases.
Highly correlated features exhibit multicollinearity. Multicollinearity can make it difficult for models to determine which independant variables are significant. I'm going to drop one of each pair of highly correlated features to resolve this.
Feature Engineering
After getting a good idea of what the data looks like, we can start making some changes to make it easier for the models to understand. There are a few phases to this section:
- Deal with missing data
- The provided dataset contains columns with a lot of missing data. In some cases this is meaningful. For example, no data in the "fence" column means there is no fence. In other cases it is simply missing.
- The missing data was filled by using a few different strategies. Ordinal columns were filled with "NA". Categorical columns will filled with the mode. Numerical columns were filled with the median of the feature, grouped by neighbourhood.
- Add new helpful features
- Sometimes adding features to the dataset can help provide important relationships to the model. For example, maybe the number of upstairs bathrooms and downstairs bathrooms is less important than the total number of bathrooms. We can add the two together and provide a new feature to the models.
- Remove non-predicitive features
- There are several features with extremely low correlation to the sale price, or contain the same value in >99% of the rows. There is little value in these features, since they seem to have no bearing on the target variable, or no relationships can be found since they are almost always the same value. These columns are dropped.
- Transform skewed features
- As mentioned, many features are highly skewed. By applying a transformation to these features, we can move them closer to a normal distribution. Here, I simply take the log of any feature with a skew greater than 0.5 in either direction.
- Encode non-numeric features
- Most machine learning models only take numbers as input. We can't train them directly on data that contain string values like "GasW" for heating type.
- Categorical features have no implicit ordering to their categories. For example, one style of roof is not above or below another type of roof. For these features we will use "one-hot encoding". This type of encoding splits the feature into multiple columns, one for each unique value present. The column corresponding to the value of the row get a "1", all other columns get a "0".
- Ordinal features do have ordering to their values. In this dataset we have ratings such as "excellent", "good", and "typical". It makes sense that "excellent" is a higher value than "typical". I apply a mapping to these features to maintain this realtionship. "Excellent" = 5, "good" = 4, "typical" = 3, and so on.
To save some space, I won't go into the details of applying all of these steps here. Please check out the notebook linked at the top of this page if interested.
Results of Log Transformation

A good example of the log transformation can be seen in the "LotArea" feature. The initial distribution is very skewed, but taking the log of each value results in a much more normal distribution.
Model Training
Now that the training data is processed, we can start defining and training some machine learning models. It's quick to train models since the dataset is relatively small, so I will train 9 different models and check the performance of each. The 9 models to be trained are:
-
XGBoost Regressor
-
LightGBM Regressor
-
SVR (Support Vector Regressor)
-
Random Forest Regressor
-
Graident Boosting Regressor
-
Elastic Net Regression
-
Lasso Regression
-
Ridge Regression
-
And finally, a stacked model combining many of the above models.
To train the models, we split the data into a training set and a validation set. The models have access to both the dependant and independent variables in the training set. Each technique uses its own methodology to find patterns in the data of the training set, using the independant variables to explain the dependant variable (sale price in this case). The models do not get to see the data in the validation set. We can feed the independant variables from the validation set into the trained models and have them predict the sales price. Since we have held back the validation set, we can then check the predictions against the true values to determine the performance of the models on new data.
To determine how well the models did on predicting the validation set, we need a quantifiable measure. Since this is a leaderboard competion, we are told that the final scores are calculated using the root-mean-squared-error (RMSE) between the logarithm of the predicited price and the logarithm of the true price. We will use this same measure to check out the validation set. After training all the models, I have them each predict the sale prices for the validation data and calculate the RMSE for each model. I also generate a blended prediction by taking the output of all 9 models and testing 250,000 randomly assigned weights for each. The lowest RMSE weights are kept.
Validation RMSE for Each Model
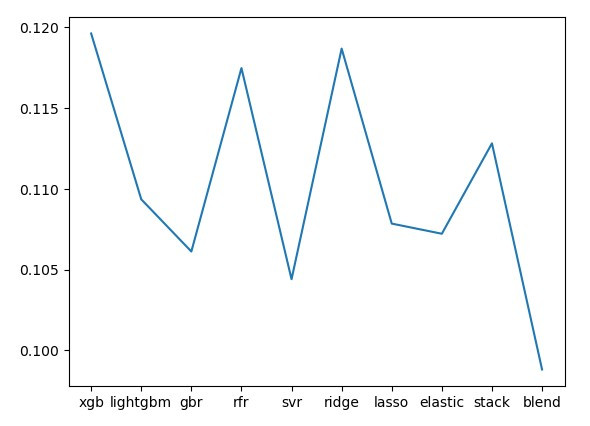
Log RMSE is comparable between all of the models, hovering around the range of 0.105-0.115. The blended model outperfomrs the others with a RMSE of 0.099. Therefore, the blended model will be used to make the final predictions.
The final step is to carry out the same data treatment as above on the test data so the test data input will look exactly the same as our training data did. The models can then make their predictions on the unseen test data and we can submit the blended predictions to the competition!
Conclusion
After submitting the notebook, the score comes back in the top 5% of the leaderboard. Not bad!

My goal for this competition was to get into the top 10%, and that was achieved. There is much that could be improved, but its an important skill to know when you've done enough to meet requirements and avoid spending time chasing minor gains. With that in mind, I consider this project complete. A few things that could be worked on if I were to return to this project are:
-
Hyperparameter tuning
-
Better weight selection for the blended model (does not converge currently, just finds a combination of weights with low RMSE)
-
More feature engineering
-
Removing more outliers
-
Trying different scaling methods; box-cox, for example.
But that will have to wait for next time!